
線形代数の入門講座、第1講は行列の種類と演算方法についてです。
行列とは
まず行列とは、数字を長方形に並べたもののことを表します。
横を行
縦を列
と呼び、縦にm個、横にn個並べたものを
m行n列の行列、m×n型の行列、m×n型行列
などと言います。
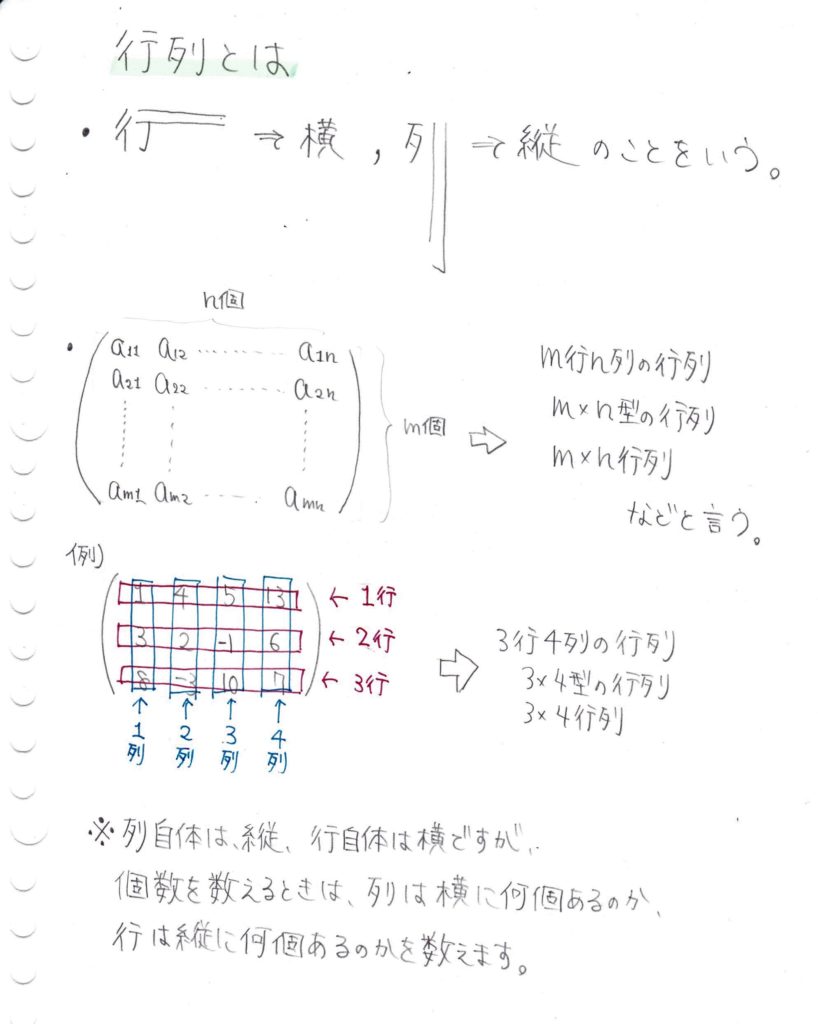
ここら辺は簡単そうで案外こんがらがるところなので、言葉の意味をしっかり押さえましょう。
行列の種類
零行列…すべての成分が0である行列のことを指す。
正方行列…行と列の数が等しい行列を指す。
対角行列…正方行列の成分のうち、対角成分以外の成分が全て0の行列を指す。
単位行列…対角行列のうち、対角成分が全て1の行列を指す。Eであらわすことが多い。
スカラー行列…対角成分が全て等しい対角行列を指す。
転置行列…行列Aの行と列を入れ替えた行列を指す。m×n行列の転置行列はn×m行列。行列Aに対して、転置行列はtAであらわす。
正方行列の中に対角行列があり、その中にスカラー行列があり、その中に単位行列があります。

行列の演算
行列の演算には和と差、スカラー倍、積の3つがあります。
和と差、スカラー倍はベクトルと同じ要領なので、すぐにわかるはずです。問題は、積です…。
和と差
行列の和と差は行列の型が等しい場合に限って定義される。
各成分ごとを足したり引いたりすることができる。(ベクトルと同じ要領)
スカラー倍
ある行列に対して、係数としてすべての成分に同じ数をかけることができ、それをスカラー倍したという。
積
2つの行列、AとBに対して、Aの列の個数とBの行の個数が等しい時のみ、積が定義される。
Aがm×n行列、Bがn×r行列の時、積はm×r行列となる。

積は、ちゃんと練習しないとこんがらがると思うので、たくさん練習をして、体に覚えこませましょう。
行列の演算に関する性質
ここでは、行列の演算の性質を紹介していこうと思います。
行列の演算は数の演算とは異なるルールがいくつも存在するので注意しましょう。
まずは、数の演算と決定的に違うところを紹介します。
・2つの行列の和差積は、必ずしも定義されるわけではない。(型が違えば定義できない)
・2つの行列A,Bに対して2つの積、ABとBAは必ずしも一致するとは限らない。(基本的にAB≠BA)
AB=BAとなるとき、行列AとBは可換であるという。
それ以外は基本的に数の演算の性質と同じです。
(以下A、B、Cを行列とし、a、bをスカラー(数)とする)
和の性質…A+B=B+A、A+0=A、(A+B)+C=A+(B+C) (→和の結合律)
積の性質…AE=EA=A、A0=0,0A=0、(AB)C=A(BC) (→積の結合律)
※Eは単位行列のことです。
スカラー倍…0A=0、1A=A、ab=a(bA)、(aA)B=a(AB)
分配律…a(A+B)=aA+bB 、(a+b)A=aA+bA 、A(B+C)=AB+AC 、(A+B)C=AB+BC
転置の性質
1.t(A+B)=tA+tB
2. t(AB)=tBtA
べき零行列…A^m=0となる自然数mがあるとき、Aをべき零行列という。