
第2講では、連立一次方程式について扱っていこうと思います。
連立一次方程式へのアプローチ
連立一次方程式を解くときに、行列が活躍します。
例題
3x+5y=9
2x+3y=14
を解け。
この問題は、高校の範囲で解こうとすると、まず一文字消去してx(あるいはy)の値をまず求め、その後y(あるいはx)の値を出すと思います。
しかしここで注目してほしいのは、文字消去をしたり、値を出したりしているときに大事になってくるのは、あくまでxやyの係数であるということです。
ということで、大学では係数だけを取り出して、行列におこして、連立一次方程式を解く方法を学びます。

ここで少し用語紹介をします。

大学ではベクトルは、手書きだと上記のように表す(パソコンの表記だとa、b、cのように太文字で表す)ことが多いので慣れるようにしましょう!
掃き出し法
ではここでは実際に掃き出し法を使った解法を考えてみましょう。
掃き出し法を使って解くときには、次の3つの変形を使います。
(1)1つの行を何倍か(≠0倍)する。
(2)2つの行を入れ替える。
(3)1つの行に他の行の何倍かを加える。
この操作を組み合わせて、
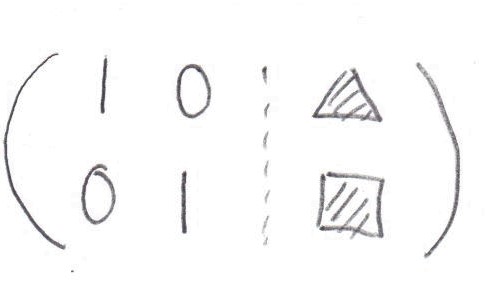
の形になるように変形していきます。
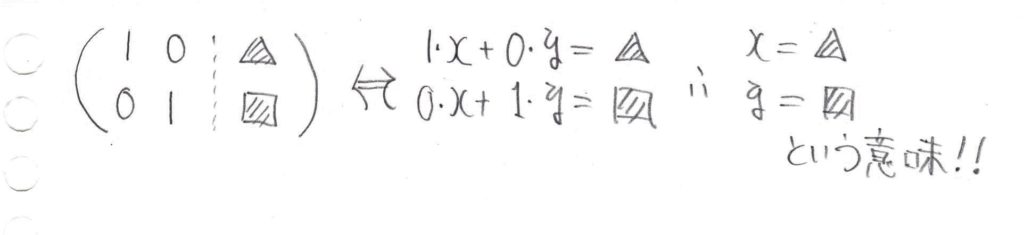
では、実際に先ほどの例題を掃き出し法を使って解いてみましょう。

どうでしょうか?理屈はつかめたと思います。
ここまでは、解がただ一つに定まる方程式を扱ってきました。
しかし、実際には
- 解が存在しない方程式
- 解が無数に存在する方程式
というものも存在します。

こういった方程式にも行列としてちゃんと答えが導き出せるように、続いて簡約化と階級について紹介します。
簡約な行列
掃き出し法では、単位行列になるように(↓)

式変形を行ってきましたが、すべての行列が必ずしもこの形になるとは限りません。
(前章最後に述べた、解が存在しない場合と解が無数にある場合がある。)
しかし、どんな行列でも簡約な行列にすることはできます。
以下の条件を満たすような行列を簡約な行列という。
(Ⅰ)行ベクトルのうち零ベクトルがあれば、それは零ベクトルでないものの上にある。
(Ⅱ)零ベクトルでない行ベクトルの主成分は1である。
(Ⅲ)各行の主成分は下の行ほど右にある。
(Ⅳ)各行の主成分を含む列のほかの成分はすべて0である。
※行の主成分…行列の零ベクトルでない行ベクトルの0でない最初の成分のこと
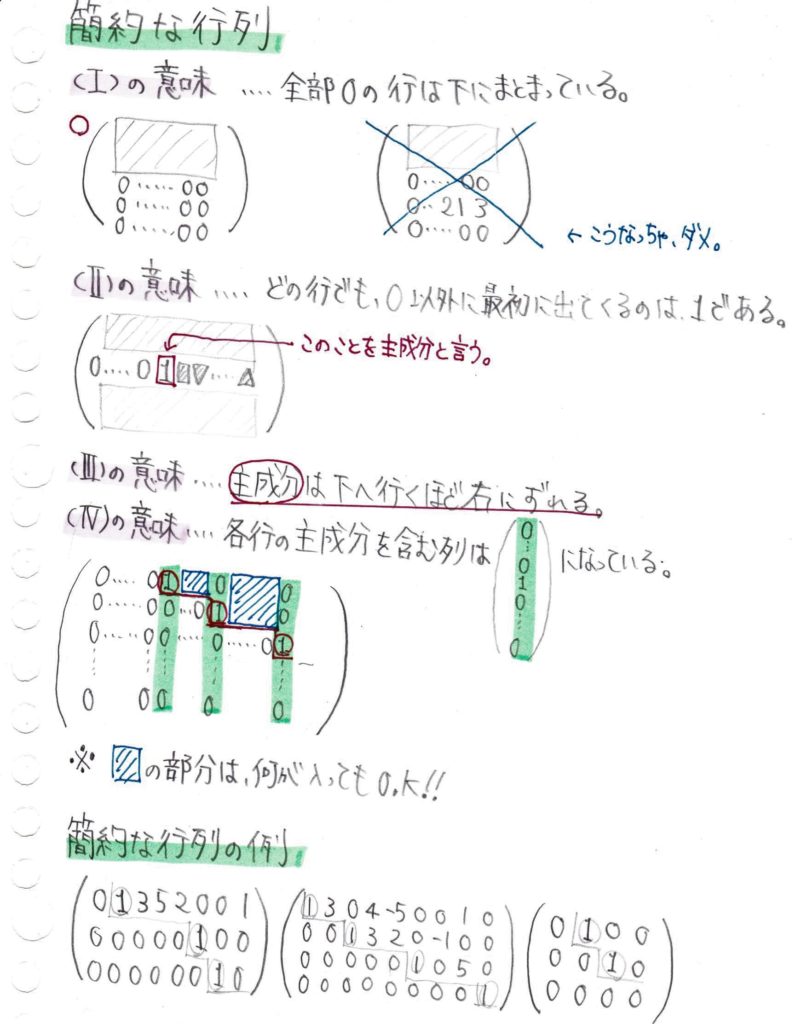
また、(Ⅰ)~(Ⅳ)までの作業を通じて簡約な行列にする作業を簡約化と言います。
どんな行列も基本変形をすることで簡約化でき、与えられた行列の簡約化は唯一通り定まります。
ここで簡約化の練習をしてみましょう。
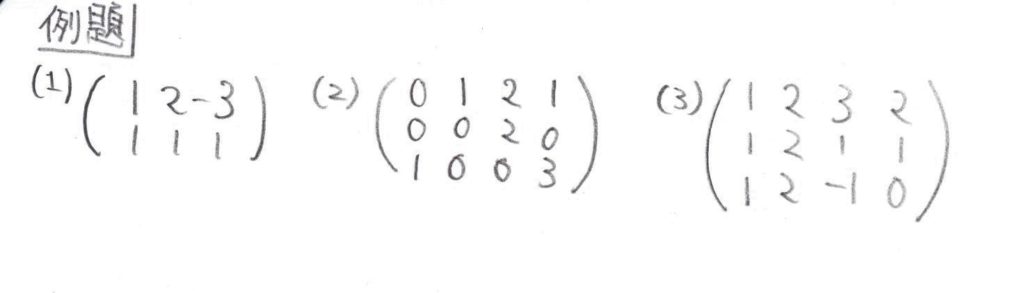

行列の階級
行列の階級…行列Aの簡約化をBとするとき、
rank(A)₌Bの零ベクトルでない行の個数
とおき、Aの階級という。
このとき、下の定理が成り立つ。
Aがm×n行列ならば、
rank(A)≦m、rank(A)≦n
この定理は、具体例を見れば一目瞭然です。

連立一次方程式を解く
以上を踏まえて、連立一次方程式を解いてみましょう。
まずは、そもそも与えられた連立方程式が解を持つのかどうかを調べる必要があります。
それを確かめるためには以下の定理が使えます。
連立1次方程式Ax=bが解を持つ必要十分条件は、
rank(A:b)=rank(A)

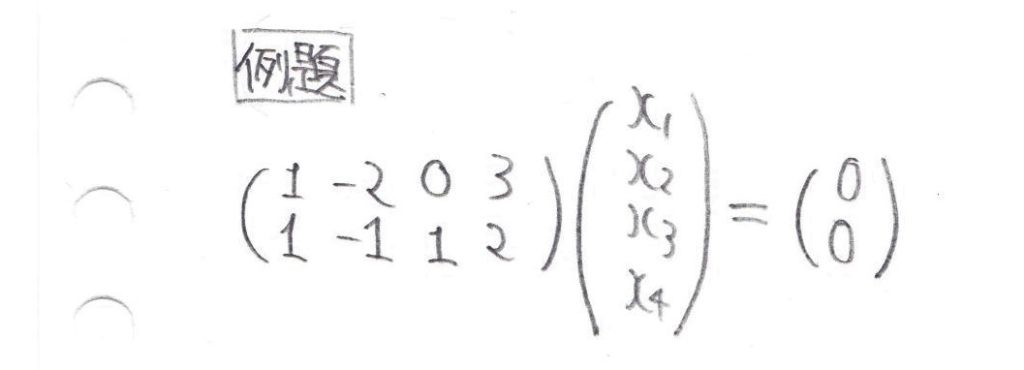
それでは早速例題を一題解いてみましょう。
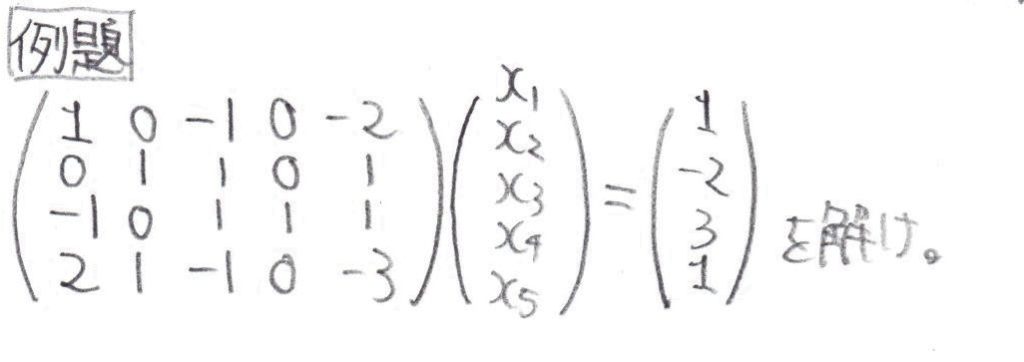
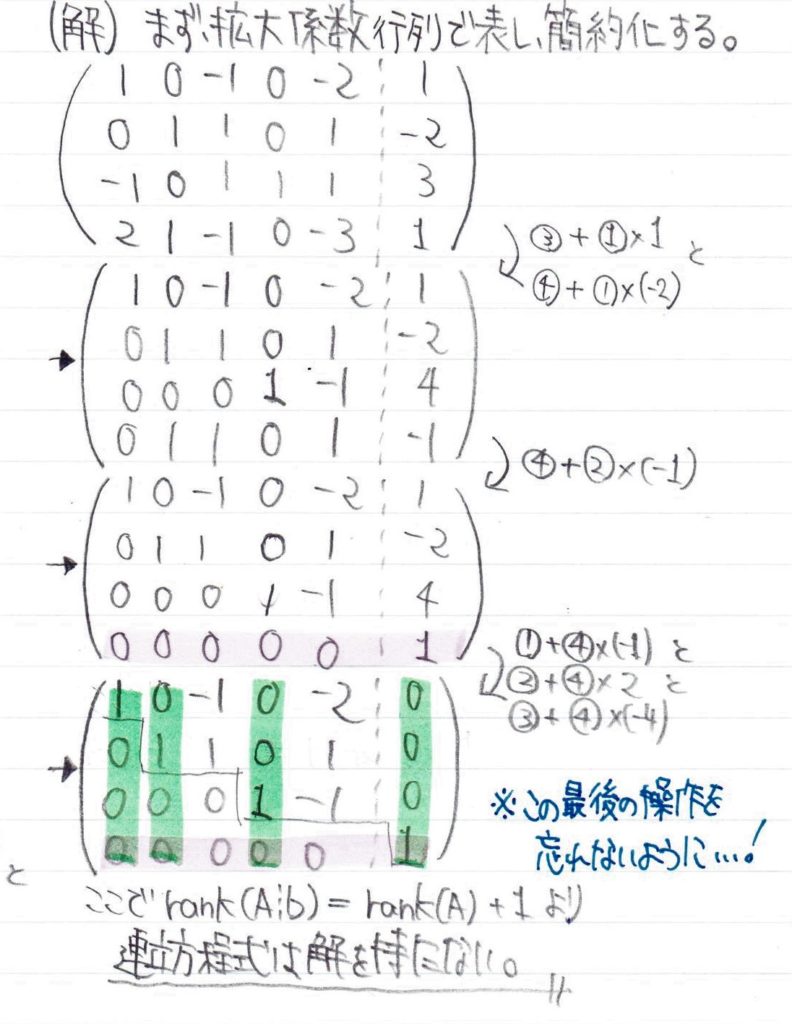
次は、解を持つ問題を解いてみましょう。
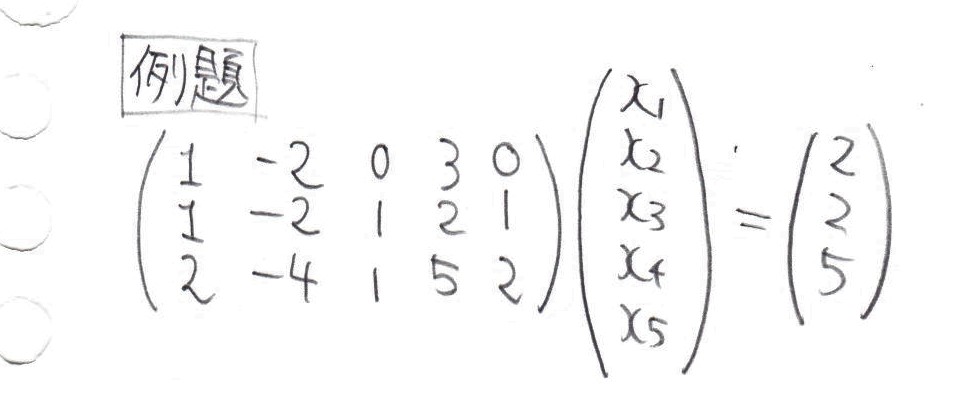
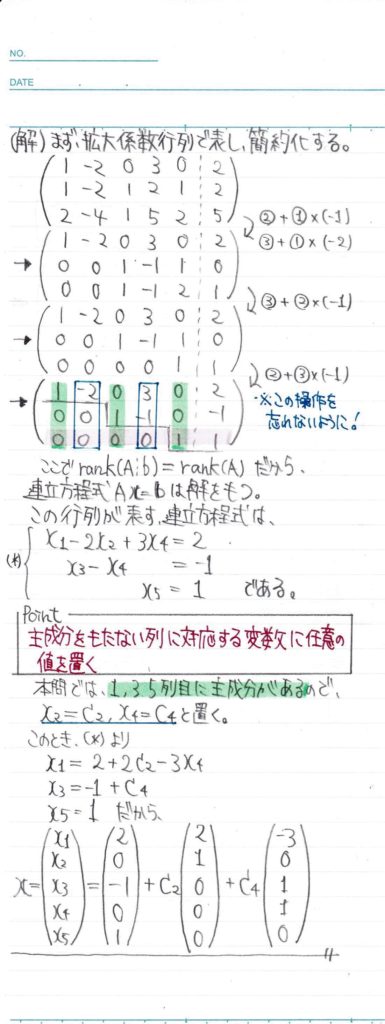
これで、解がただ一つに定まらない場合の連立一次方程式が解けました!
逆に、解がただ一つしかないときはどういうときでしょうか。
ここで、解の自由度というのを定義します。
解の自由度…連立方程式を解いたときに現れる文字の個数のこと。
上の例題では、C2とC4の二つの文字が現れているので、解の自由度は2になります。
この時、
解がただ一つ定まる⇔解の自由度は0である
ことは自明です。
(∵一つでも任意の定数があれば解が複数個できてしまう)
以上から、以下の定理が成り立ちます。
n変数の連立1次方程式Ax=bに解がただ一つ存在する必要十分条件は、
rank(A)=rank(A:b)=n
である。

また一般に
(解の自由度)=n-rank(A)
で表せます。
補足
連立一次方程式Ax=bにおいてb=0のとき、すなわちAx=0の形の連立一次方程式を同次形の連立一次方程式という。
また、同時形の連立一次方程式はいつでもx=0の解を持つ。これを自明な解という。
ここで以下の定理が成り立ちます。
Aはm×n行列とする。
(1)Ax=0 の解が自明なものに限る⇔rank(A)=n
(2)m<nならばAx=0は自明でない解を持つ
難しい説明は置いといて、要するに
同次形の方程式(b=0)では、拡大係数行列を使わなくても、係数行列だけで解ける!
と覚えておきましょう。

まとめ
長くなりましたがまとめです。

演習を積んで、ぜひ自分のものにできるように頑張りましょう!
2020/7/15