
第4講では、置換について扱っていきたいと思います。
置換
置換…n文字の並び替えに対応する写像のこと。σで表す。
n文字の置換は、n!通りあり、そのすべてをSnで表す。

※この書き方は、上下の組み合わせが同じなら順序は変えてもよい。(行列と大きく違うところ!)また、動かさない文字は省略してもよい。
置換の積
まずは定義から書いていきます。
2つのn文字の置換σ、τの積、στは、
στ(i)₌σ(τ(i)) (i₌1,2,3…,n)
で定義される。

※のように毎回書くのは面倒なので、コツをつかんで簡単に置換できるようにしましょう。


順番を逆にしたら、結果が変わるので気をつけましょう!

では、置換の積の演習問題を1題解いてみましょう。

単位置換、逆置換
・単位置換…すべての文字を動かさない置換。εで表す。
・逆置換…順番がちょうど反対になっている置換のことを表す。
置換σに対し、σ-1で表し、σσ-1₌σ-1σ₌εで表される。

巡回置換
くるくるサイクリックに回る置換のことを巡回置換と言います。
巡回置換には以下の性質があります。
任意の置換は共通部分のない、巡回置換に分解することができる。
そして巡回置換は下のように表記します。

互換の積
巡回置換のうち、特に2文字の置換を互換と言います。
そして以下の法則が成り立ちます。
任意の置換は互換の積で表せる。
互換の積っていうのは、簡単に言えば入れ替えの組のことです。
入れ替え方は人それぞれですが、入れ替え方の回数の偶奇は必ず一致します。
また、互換の積は下のように書きます。

互換の積について例題を解いてみましょう。
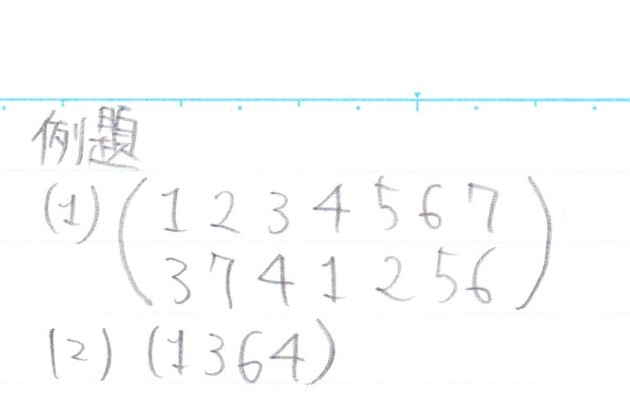
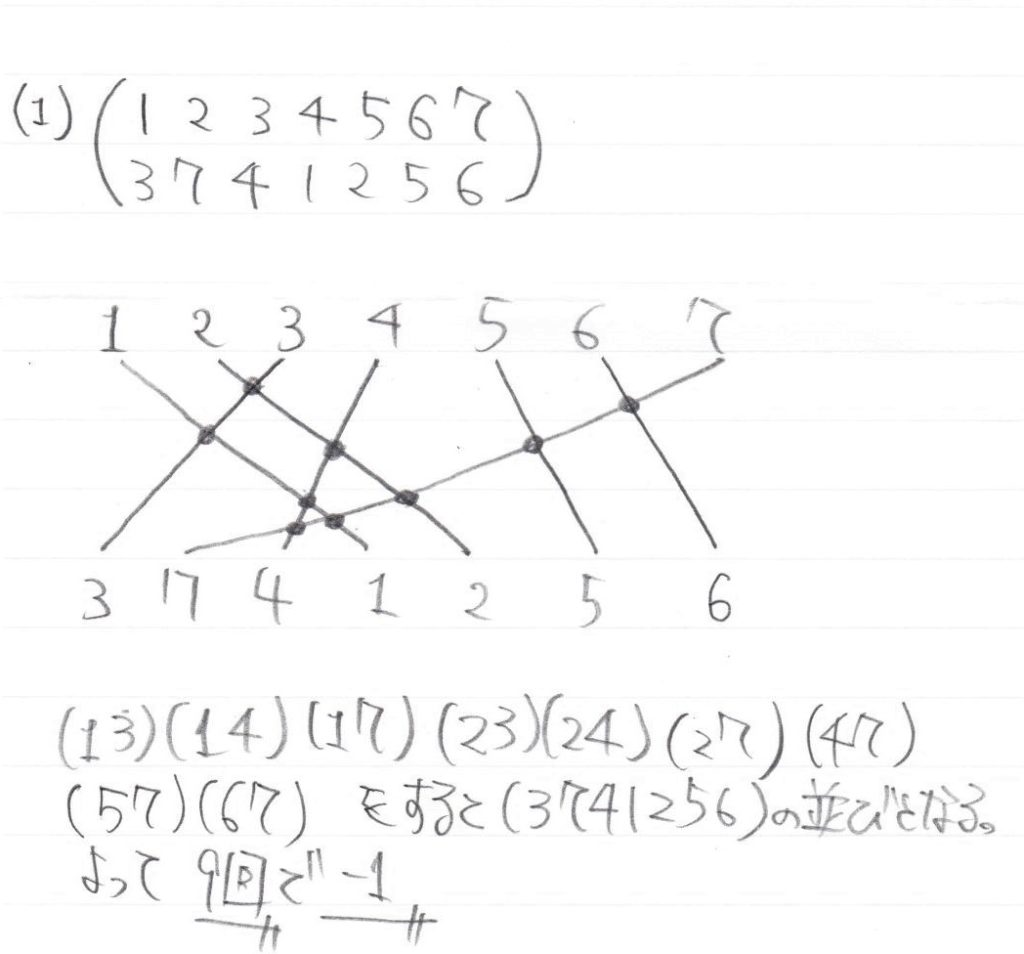
(1)は説明通りですね。

(2)はまず置換の形に直す必要があります。
そこからは説明通りの流れになります。
この時のイメージとしては、置換するときの置換後(ゴール)をまず問題から解いて、スタート(123…の並び)からゴールまで互換のみで行くことを考えます。
※置換の積についての補足
「置換の積を求めよ」という問題は、最初の置換の積の章で紹介したような書き方(オーソドックス)で出題されることもあれば、「巡回置換」や「互換の積」の形を絡めて出題されることもあります。
(そもそも置換の積というくらいだからいくつかの置換の変遷を組み合わせれば何でも置換の積となります)
だから置換の積とは広義には右から置換操作をしていくことを総称していると思っておいてください。
まあ具体例を見ればわかると思うので、以下に例題を用意します。
是非考えてみてください。

まずは(1)です。
これはオーソドックスな形ですよね。

(2)は一瞬戸惑った方もいるのではないでしょうか。
でも焦らずに定石通り右から互換していきましょう。

ここも順番に左から操作していきましょう

置換の符号、偶置換・奇置換
置換の符号は、
sgn(σ)₌(-1)^m (mは互換の積に分解された個数)
で表せる。
そして、sgn=-1なら奇置換、 sgn=1なら偶置換と言います。

2020/8/15